CMU-深度学习系统-第六章

• 全连接网络
• 优化器
  • 牛顿法
  • momentum（动量）
    • 无偏动量
    • Nesterov动量
  • Adam
  • 随机抽样
• 初始化

这一章主要是讲全连接网络，优化器，初始化。

全连接网络

也叫MLP，多层感知器，之前章节里没有bias，这一章加上了

常说的网络参数，也就是把权重和参数合起来。L代表层数

在考虑运算的时候，维度很重要，正确的写法是

因为如果，那么bias肯定是矩阵，但是实际上是一个n个元素的向量，所以要在上乘一个m行1列的全1矩阵进行广播。

对于全连接网络，很重要的是如何挑选优化器和初始化权重，也就是接下来两点讨论的内容。

优化器

最终目标是找到让最小的值

传统的梯度下降法采用不同的超参会得到不同的收敛结果：

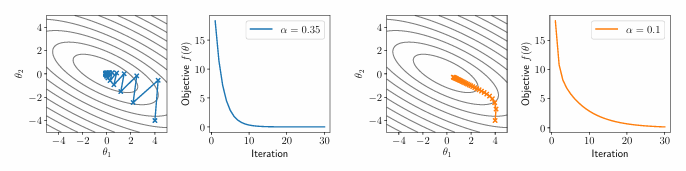
但是这样还得尝试不同的超参，我们目标是花费尽量少的时间找超参。因此出现了带动量的一些方法。

牛顿法

只作为了解，因为用得少。

牛顿法继承了更多的全局结构，加入了Hessian矩阵，即二阶导数矩阵，来调整梯度下降（放缩原梯度），在凸函数中逼近最低点，公式如下：

等效于使用二阶泰勒展开将函数近似为二次函数，然后求解最优解。如果的话就是牛顿法，否则叫阻尼牛顿法。

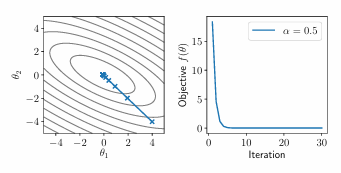
可以看出完全没有震荡，直接就是最低的方向。但是实际上不常用：

1. 求二阶导效率太低，而且存储空间太大
2. 对于非凸优化来说牛顿法似乎用不上

momentum（动量）

是一种更容易计算，但是也部分考虑了全局结构的方法，更常用一点。

更新的公式如下：

通过来对此前的梯度求一个移动平均值，然后用这个平均值来更新梯度，这样可以减小往其他方向的震荡，增大最大方向的速度。

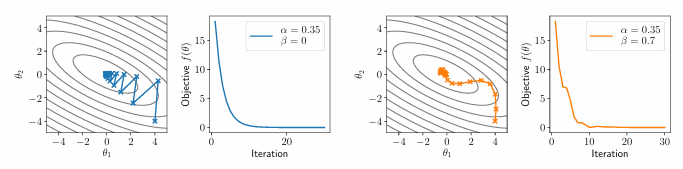
无偏动量

因为往往初始化为0，这样的话就会带来最初的更新缓慢

加上去除偏差项（放缩项），让每次更新的步伐大致类似，公式如下：

可以看见每一次梯度更新都会平衡一些之前梯度的影响，放大本次梯度的作用。

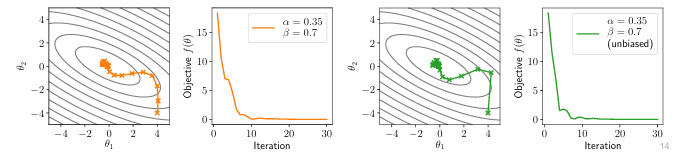
Nesterov动量

原本的动量更新是使用本次的梯度，这个使用更新后下一个点的梯度来更新，其实数学原理我也不太懂，但是从结果上来看似乎更加平滑了。

对凸优化有用，有时候在深度网络中有用。

Adam

不同层之间的梯度尺度可能变化较大，因此提出的自适应梯度方法（adaptive gradient methods），它捕捉不同梯度间的尺度变化，调整梯度更新的比例。

这是最常用的方法，包含动量和自适应。更新公式如下：

这个方法包含两个动量，用来捕捉梯度的变化（和之前的作用一样），用来估计梯度向量幅度的平均值（我觉得有点像方差那个意思）。是微小干扰，防止除以0。这一项把梯度放缩到相似的尺度。

随机抽样

以上都是说的整体，但是最重要的并且最可行的肯定是一小部分一小部分更新，即小样本计算梯度可得到有噪声但无偏的梯度估计，是重要的优化策略。

对比SGD：

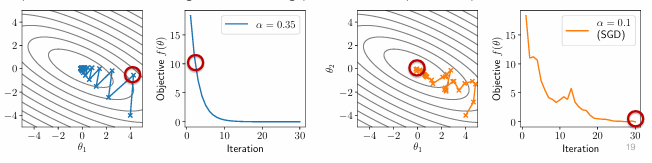
虽然有噪声，但是廉价，可用。

初始化

如何初始化参数？全取0吗？并不是，因为全0在深度学习中是鞍点。如果初始化为全0，那么梯度也会全0，因为激活函数会让所有值都是0

所以一个很关键的点时，选取初始化值很重要。

如果选择所有的梯度服从一个正态分布，这个正态分布的方差很重要，影响前向传播的激活值以及梯度的变化

norm是范数，其实就可以简单理解成大小我感觉

下图是在 MNIST 数据集上的示例，使用 n=100 个隐藏单元，网络深度为 50 ，激活函数为 ReLU

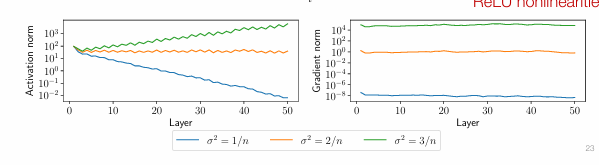
可以看到2/n的方差最好，因为每一次经过激活函数会有大概1/2的值被激活函数变为0，如果取方差是2/n就能保持稳定传播，n为隐藏单元的数量

如果使用 ReLU 非线性激活函数，的 “一半” 分量会被设为 0 （因为 ReLU 函数对于负输入输出为 0 ） 。为了在使用 ReLU 后能得到和线性激活时相同的最终方差，需要将 的方差加倍，所以 ，这就是何凯明正态初始化（Kaiming normal initialization ）的原理

第二个关键点，解释了为什么初始值很重要，实际上深度学习的训练过程会让权重变化没有那么大，相对而言最终权重离初始值更近，而不是每次都收敛到相似的区域